
Gelenkwelle mit elastischem Zwischenwellenlager
Keine Vibrationen – Ein gutes Gefühl beim Fahren
Vertrauen Sie bei dem Zwischenwellenlager auf das eigens entwickelte Dichtungskonzept der Eugen Klein GmbH.
Verfügbar von 9.500 Nm bis 35.000 Nm.
Zeichnung
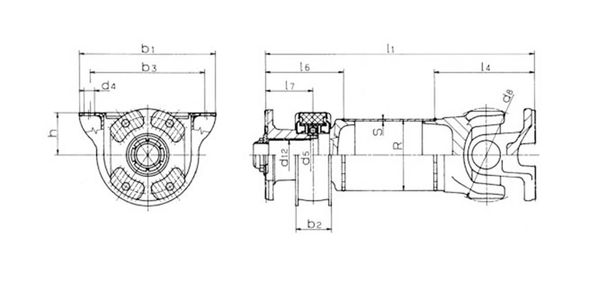
Technische Details
| Funktionsgrenzmonent MFG | Nm | 9500 | 14000 | 17000 | 25000 | 30000 | 35000 |
| Bauart und Baugröße | Nm | 026 376 | 026 490 | 026 590 | 026 620 | 026 680 | 026 700 |
| Gelenk-Rotations-Ø d8 | mm | 138 | 158 | 172 | 178 | 204 | 204 |
| Flansch-Ø d1 | mm | 152 | 152 | 180 | 180 | 180 | 180 |
| Höhe l3 | mm | 86 | 82 | 85 | 92 | 100 | 100 |
| Dicke e1 | mm | 16 | 16 | 18 | 18 | 18 | 18 |
| Schraubenloch-Ø d3 | mm | 13,0 | 13,0 | 15,0 | 15,0 | 15,0 | 15,0 |
| Rohr-Ø RxS | mm | 85x5 | 120x3 | 120x4 | 120x6 | 140x5 | 140x5 |
| Maximaler Beugewinkel ß | Grad | 35° | 25° | 25° | 25° | 25° | 25° |
| Mindestlänge l1 | mm | 410 | 400 | 415 | 475 | 475 | 500 |
| Gelenklänge l4 | mm | 171 | 169 | 182 | 192 | 220 | 225 |
| Lagerzapfenlänge l6 | mm | 141 | 132 | 132 | 182 | 165 | 181 |
| Lagerabstand l7 | mm | 95 | 80 | 80 | 107 | 107 | 107 |
| Lager-Innen-Ø d5 | mm | 65 | 65 | 65 | 75 | 60 | 70 |
| Höhe h | mm | 71,5 | 71,5 | 71,5 | 85,5 | 88 | 88 |
| Gehäuselänge b1 | mm | 230 | 230 | 230 | 255 | 255 | 255 |
| Gehäusebreite b2 | mm | 60 | 60 | 60 | 60 | 65 | 65 |
| Schraubenloch-Ø d4 | mm | 15 | 15 | 15 | 15 | 15 | 15 |
| Schraubenlochabstand b3 | mm | 200 | 193,5 | 200 | 220 | 220 | 220 |
| Zahnwellenverbindung DIN 5480 d12 | mm | 55x2,5 | 55x2,5 | 55x2,5 | 50x2,5 | 60x2,5 | 70x2,5 |
| Gelenktragzahl T | Nm | 2260 | 2800 | 3490 | 4435 | 5100 | 6850 |
| Gewicht bei l1 = 1000mm G | kg | 24,0 | 26,0 | 32,0 | 40,4 | 44,1 | 52,3 |
| Gewicht von 100mm Rohr GR | kg | 0,987 | 0,865 | 1,144 | 1,687 | 1,665 | 1,665 |
| Massenträgheitsmoment bei l1 = 1000mm Jm | kgm2 | 0,0472 | 0,0706 | 0,0949 | 0,1214 | 0,1718 | 0,1879 |
| Massenträgheitsmoment von 100mm Rohr JmR | kgm2 | 0,00158 | 0,0029 | 0,0038 | 0,0054 | 0,0076 | 0,0076 |
Weitere Flanschspezifikationen können auf Anfrage gefertigt werden.




